Words

Hi,
this is the first in a series of articles where I will cover some technical problems and solutions that occurred to me during the development of my game Syzygy. The fact that these problems presented themselves in the first place depends on a long and articulated series of game design decision that will be taken for granted and will not be discussed in these posts.

But first of all, we must at least clarify what the game is about. Syzygy is a puzzle game centered around the possibility of changing the connectivity of a grid-based map from squares to triangles and hexagons at any moment. That’s quite a mouthful, see the following gif for a visual clarification:

From this basic concept, it is possible to articulate many puzzles, mainly centered around how you and other types of creatures can (or cannot) move in such a peculiar environment. Given that, all visual elements should contribute to the changing shape of the world: the map as well as the characters’ appearance and the background.

In this first post, we will focus on how the map can transition smoothly from one shape to the other; leaving the other topics for next time.
To tackle this first point, we must introduce the concept of geometrical tessellation.

Tessellation

A tiling or tessellation is the covering of a plane using one or more geometric shapes with no overlaps and no gaps. From mere trial and error we can easily see that there are only three ways to tessellate a plane using a single regular polygon, that is, using triangles, squares or hexagons.

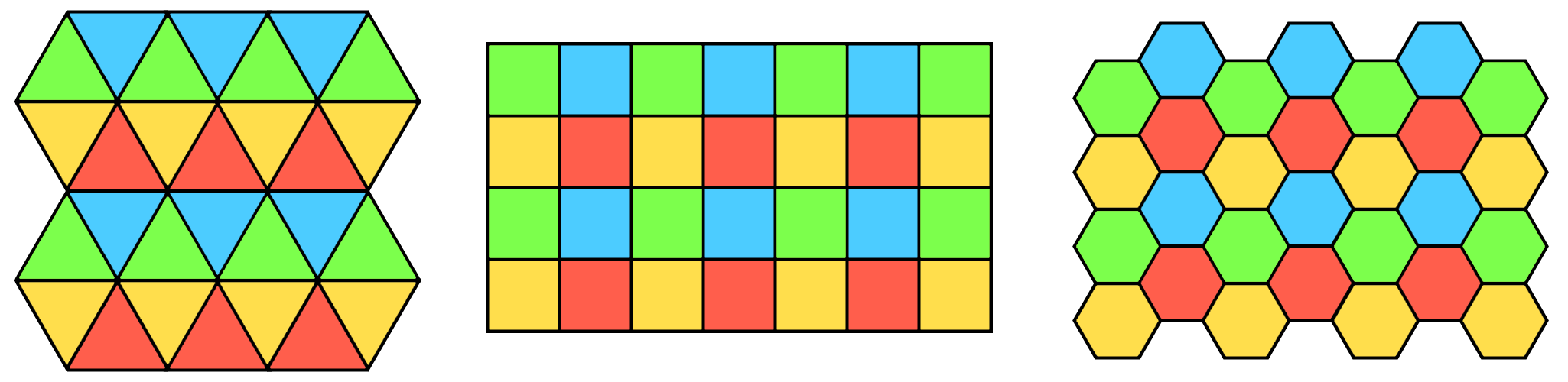
A square tiling is highly symmetric while the other two not so much, leading to a couple of different arrangements. To have a consistent transition (and consistent gameplay!) we have to establish which of the possible variants we want to use: in my case, the top-left triangle have its tip upwards and the first column of hexagons is lower that the second one.

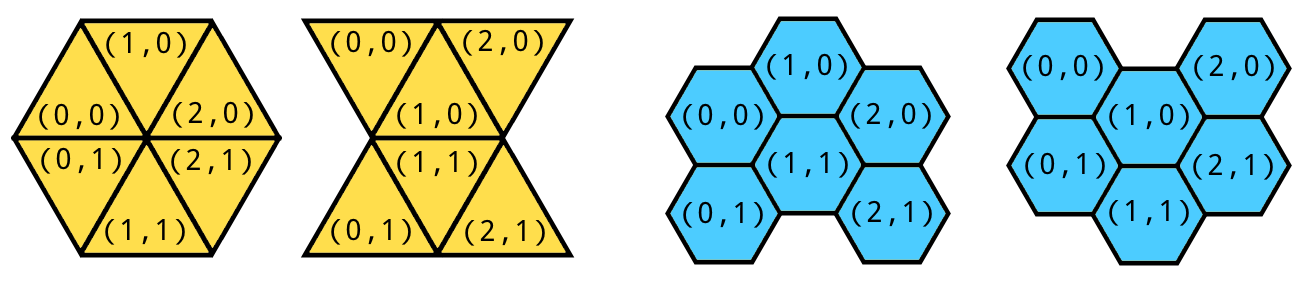
Tessellation done by means of a single regular polygon is usually called a regular tiling. As a side note, cubes are the only regular solid able to tessellate the space, so a 3D version of Syzygy would make no sense whatsoever.

Obviously, using more than one shape or even keeping just one shape but using various sizes of it creates a number of new tilings. Extending the search to all polygons, instead that forcing ourselves to use only regular ones, let us discover that there is an infinite amount of tilings and that’s exactly what we want for our transition animation. To be more precise, we actually need three animations: one for every pair of shapes.

The basic concept of all three animations is to linearly interpolate (lerp) between the vertices of the two extreme shapes to obtain a new shape, that is also a tessellation for every step of the lerp. I designed the transformation so that the area of a shape is constant across changes: it is not mathematically required to do so (e.g. it is possible to lerp from small triangles towards big squares), but it felt better this way since the whole grid remains approximately of the same size.
Let’s see how to make it work case by case.

Triangles to Squares

In this transition, the tip of the triangle is split in two and the four vertices so obtained are lerped towards the positions they have in a square. As the shapes change, their center positions need to change too: luckily, this can also be taken care of with a simple lerp from the centroid of the triangle towards the centroid of the square.

Squares to Hexagons

This transition is fairly similar to the previous one: two vertices are added at the top or at the bottom of the square, depending on which column the shape lies on, and then the vertices are simply lerped into place. Notice that in both this animation and the previous one I am using only one shape that gets appropriately rotated, depending on the position it occupies on the grid.

Hexagons to Triangles

This is a little trickier. I have not bothered trying to prove it as a theorem, but I am pretty sure that it does not exist a way to lerp from hexagons to triangles using a single polygon, since the obtained one is not a tessellation.

This is not really a problem though: it was neat as long as it lasted but I was never really against having more than one shape during the intermediate tessellations. In this case, two shapes are sufficient: they must be interlaced on alternate rows.

As I stated earlier, the number of vertices per shape is bound to change during every transition but, since my biggest concern is having a consistent framerate, I always draw six vertices for every shape even when triangles are selected; some vertices will be overlapped, but it’s ok.

And with this last remark, we have concluded the taxonomy of shape transitions. Any single one of them lasts 300 milliseconds in game, so they are barely visible. But, since the player is going to change shape all the time, I think it was worthwhile to make them as smooth as possible.

Thank you for keeping up till the end and I hope it has been an interesting and insightful reading. Stay tuned for the next part, in which we’ll talk about how sprites are rendered and animated.

Hi,
welcome to the second in a series of articles where I talk about some noteworthy technical problems I encountered during the development of my video game Syzygy. In this part, we are going to address how sprites are rendered and some interesting consequences that arise from the method used.

Remember that our initial goal was to have every element in the game reflect the change in shape and we put quite some effort into animating the game map. A really simple idea comes to mind: maps are made by square tiles and sprites are made by square pixels; therefore, we can just draw the sprites as if they were maps. The small caveat is that we must reduce to zero the spaces between shapes, making them all contiguous.

Obviously, turning every pixel into a full-fledged polygon is very costly, but there are some mitigating factors that render the whole endeavor possible:

1. sprites are extremely small (never more than 32 pixels in any dimension, often much less);
2. being a puzzle game, levels tend to be small and with only few moving pieces;
3. GPUs are fast and the task at hand is much lighter than drawing an entire 3D scene in a triple-A game.

The frame rate still tends to drop for old laptops with integrated graphic cards but, being Syzygy a meditative game with little action in it, having a consistent frame rate is enough to guarantee a smooth player experience. I plan to expand on this topic in the next part, but for now it is sufficient to say that for any modern hardware the game can run at 60 fps with little effort, even without custom optimizations on my part.

Since I were at it, I went on and made a pixel art font rendered with the same method as sprites are. In the end, everything in Syzygy is drawn based the current shape, even the menus and GUI buttons.

Problems

It all looks quite fine on paper, but in reality just producing pixel art assets and drawing them using different shapes resulted in the most ugly and deformed characters imaginable.

On hexagons, outlines and lines of pixels tend to be broken in many places, producing an unpleasant effect; while, on triangles, badly placed pixels make the sprite look as if it was full of spikes. The following example is so distorted that a smiling face is turned into a sad one.

This phenomenon is especially bad in the pixel-art font, where letters change so drastically that they can morph into complete garbage. Below, you can see the letter X as an example: on top the naive version, on the bottom what I find to be the best looking option.

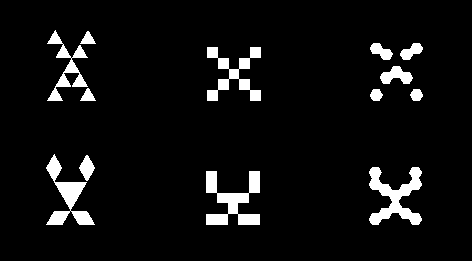
To help me mitigate this problem, I built a small tool that just shows how a sprite would look in any of the three shapes at the same time, so that I could keep it open while drawing to have immediate feedback on the changes I was making.

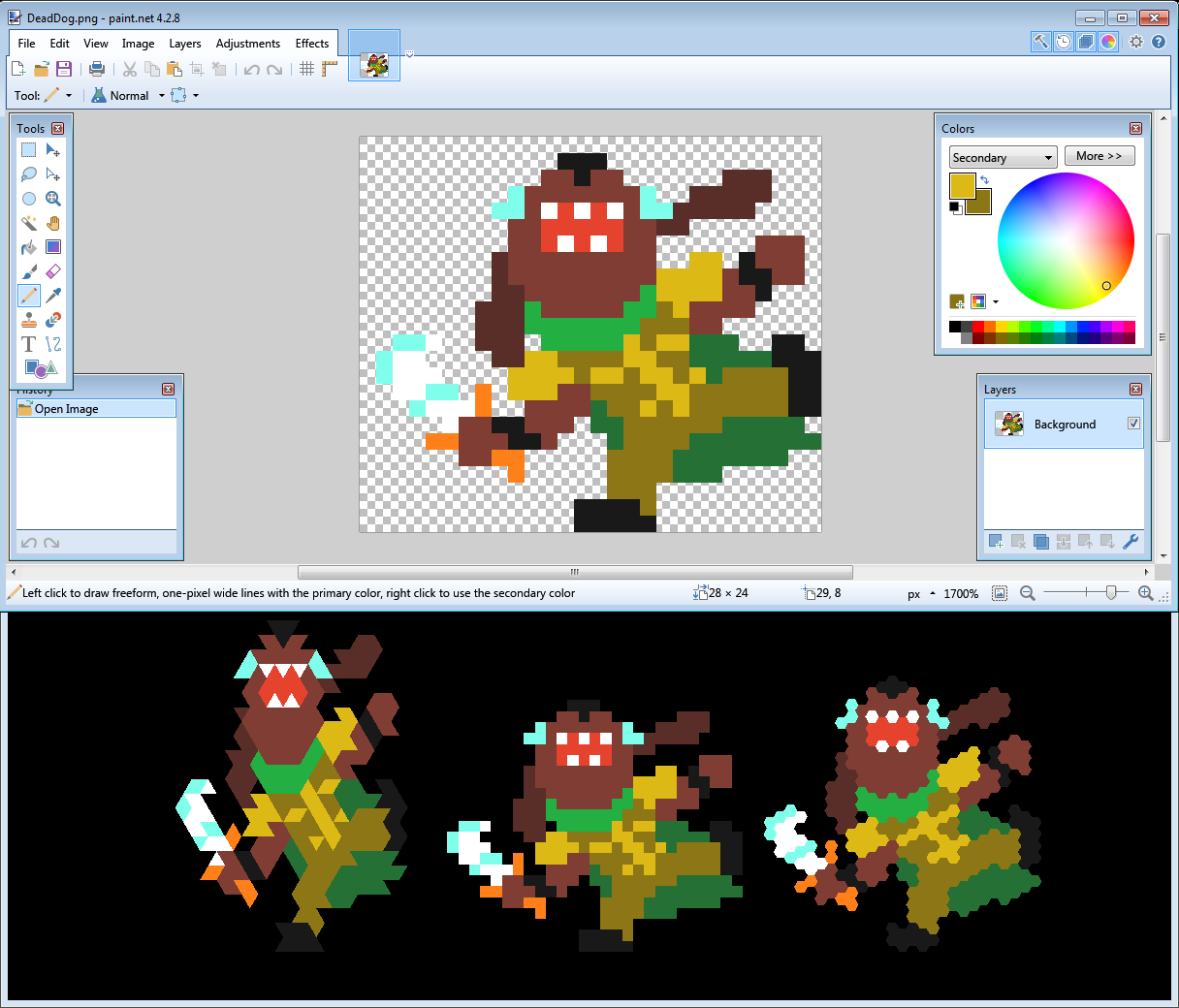
Working with this tool soon brought me to a couple of realizations: the first one was to remove all outlines, because there was no hope of making them work, and the second one was a simple trick that somewhat reduced the constraints I was subject to.

In the previous part, we talked about how we had to pick which columns were higher on the hexagons and if the first triangle had its tip upwards or downwards. Well, it turns out that we can introduce an offset in both x and y to alter this choice and make the sprites look slightly different. It is also possible to use offsets that keep unchanged the triangular version, while modifying the hexagonal one, and vice versa.
More precisely, the change is subject to the following equations:

column_high = offset_x mod 2
tip_down = (offset_x + offset_y) mod 2

leading to four possible combinations:

• Tip up and column low -> offset (0, 0)
• Tip down and column high -> offset (1, 0)
• Tip down and column low -> offset (0, 1)
• Tip up and column high -> offset (1, 1)

This is very useful because it means we can pick the best looking polygon arrangement for every shape and, if something looks bad in a certain position, we can try to offset it to make it look better.

As a side note, this technique also becomes useful while designing a level to make the map have certain constraints in specific positions. This last statement implies that the game world is not invariant for translation: offsetting a level by one tile effectively creates a new level with potentially different solutions.

Animations

As we said, drawing a polygon for every pixel in the game is costly, but it also gives us complete control on those pixels, allowing us to produce some neat graphical effects basically for free. I tried to exploit this peculiarity as much as possible in various animations. Let’s see a few examples.

Fade

A very simple one is the fade in/out effect: every pixel is shrunk progressively, making the sprite disappear. In game, all these animations are pretty fast, having a length measurable in tenths of second, but the effect is still fairly perceivable.

Teleportation

When transitioning from a level to another, the player and text disappear with a “teleporting” effect where the topmost pixels are sent flying upwards and their dimension is progressively shrunk until they disappear. This is repeated row by row until the entire sprite is removed from view.

Explosion

The death animation is a disgregating explosion in which the sprite is rapidly magnified while the size of every single pixel is decreased even faster.

And with this animation showcase we conclude our analysis of sprite rendering.
Thank you for your time and I hope it has been a fun ride. Stay tuned for the last part: a mixed bag in which we’ll talk about backgrounds, resolution, color blindness and optimization.

Hi,
welcome to the last in a series of articles where I discuss technical issues I had to overcome while working on the visuals of my game Syzygy. In this last part, we will tackle various miscellaneous topics that where left out in previous instances: every one of them is structured like a standalone chapter, so feel free to read only the ones you are interested in. Let’s start with how the game background works.

Background

The main constraints envisioned for the backgrounds were the following:

1. to be filled by procedural patterns defined as functions that take the position of a cell and return a color value;
2. to have a unique one for every level;
3. to look like a sea.

These requirements demanded a solution that could potentially have a very large number of variations, but deterministic in nature. I initially thought about using fluid-simulating cellular automata or fractals, but both turned out to be too computationally intensive and poorly controllable.

In the general sense, they also have something else in common: they are physically complex. Complexity in physics is usually defined, quite dramatically, as what stands at the edge between order and chaos.

In more prosaic terms, imagine that you want to classify various systems based on their observation. A system is treated as a black box function W(t) that at a fixed timestep t produces a single value. A system trace is defined as a tuple of the observations (W(0), W(1), W(2), …). Now, let’s consider a few examples and try to classify them:

• (1, 1, 1, 1, 1, …) is an extremely ordered trace; it is always constant and can be trivially described;
• (1, 2, 1, 2, 1, …) is also an ordered trace, because it can be easily described as alternating ones and twos;
• (68, 87, 12, 73, 44, …) is instead a chaotic trace; the numbers contained are completely random, there is no unifying way to describe them;
• (1, 0, -1, 0, 5, …) may be considered a complex trace; the pattern is somewhat perceivable but it is hard to grasp.

If we substitute t with our cell coordinates (x,y), you can see we are starting to get somewhere. Now, we know we would like to have a function that produces a complex trace; but if we can’t have trace 4, I’d say we should prefer trace 3 to trace 1.

Computers are deterministic in nature so they cannot really produce true randomness: instead, it is possible to build a family of functions, called pseudo-random functions, that behaves a lot like random numbers but are instead deterministic. If you know a little bit about pseudo-random generators, you also know that it is hard to build a good one. In fact, it is very easy to inadvertently introduce some kind of pattern in the sequence of numbers.

But, in our case, this is exactly what we want: if we use a very bad pseudo-random function to generate the background, we obtain a repeating pattern that is diverse enough to be appealing. More precisely, we use this basic structure:

W(x,y,t,modulus) := 0.5 * ((f(x,y) mod modulus) / (modulus – 1)) + 0.5 * unit_sine(t)

Since the hue and saturation are both defined a priori, we really just need the intensity of our color, so the codomain is [0,1]. We compute the modulo operator because it is one of the simplest and worst ways to obtain a pseudo-random number. The unit_sine function is accountable for the sweeping sea-like motion in the background. To make every background unique, we also apply a different arbitrary function f to the (x,y) coordinates of cells to each one. Let’s see a couple of examples in action to clarify the whole concept:

f(x,y) = x² + y²

f(x,y) = x + 2 * y

More on Tools

One recurrent notion that became evident during development is how precious tools can be. In part two, I talked about the drawing tool that allowed me to visualize sprites on different shapes at the same time, but I also developed various other small programs that really helped me.

To speed up the level design, I built an pretty standard editor that allowed me to quickly create levels, experimenting with the mechanics without being slowed down by having to edit text files.

The profiler is another pretty standard tool that allowed me to measure function time and optimize accordingly, which is incredibly valuable when trying to get a consistent framerate.

Let’s open up a not-so-small side note on framerates. As you may have already noticed in you everyday life, humans tend to be sensible to the derivative of quantities more than to the quantities themselves. Human attention is far more triggered by what changes than by what stays constant.

If you enter in a room filled to the brim with pots, you will certainly notice it and maybe examine the most peculiar ones for some time. But if you stay there for hours or days, you will pay increasingly less attention to them as time goes by, to the point where you won’t even realize consciously they are there anymore.

To a certain degree, everyone tends not to notice static objects, constant background noise, persistent smells, etc. So when your framerate drops from 60 to 45 fps (frames-per-second) you notice the game lagging, not because 45 fps are not enough but because you have perceived an alteration in the framerate.

To ensure the most consistent framerate possible, I set up Syzygy to draw at startup a heavy test screen in a hidden window: so heavy, in fact, that it is more computational intensive than the most computational intensive scene in the entire game. By measuring the rendering time for this scene, the game is able to deduce the optimal framerate for the current machine and then run at that framerate from then on.

To verify my assumptions, I recorded the computed framerate in a log file and asked all my testers if the game ever lagged while they where playing. Reasonably, for testers who consistently played at 60 fps the answer was “No”. This was also true for people who played at 30 fps.
What I did not expect was that some of my friends with really old machines played the whole game at 15 fps and they all claimed to have never experienced any lag whatsoever.

Certainly, the game’s genre contributed to this result: when solving a puzzle you are more concerned with your reasoning than with the game smoothness. Doing the same experiment with an action game might lead to a very different outcome but, still, it seems to me a really valuable piece of information to carry along.

The peak is Windows preparing to take this screenshot.

The last entry on our tour is an incredibly useful program that greatly simplified my testing process: a playthrough recorder. The concept is simple: while the game is running, on every frame, the input data structure is dumped to file along with a few other data like window size and position; then I have these files sent back to me by testers and I can then replay the entire playthrough on my copy of the game at any speed I want.

This is extremely useful because it’s almost as good as being side by side with the tester while she is playing; with the added benefit that not being in the same room lifts a lot of the psychological pressure of performing well while being watched.

It’s a simple and effective technique to catch bugs and design flaws alike: the caveat is that, at least my implementation, it ended up being somewhat sensible to window resizes and movements, getting to a point where, when the user clicked just at the border of a tile, it worked on her computer but in my replay it didn’t. I believe it is a bug related to the Windows API used to set the cursor position, but I didn’t take the time to sort it out: forcing the game to be full screen for all testers actually resolved the issue and I assessed it to be a good enough fix for non-shipping code.

Nonetheless, when I’ll reimplement the tool for another game, I will not record the input structure directly, but instead use the actual actions performed in the game: I think going up one level of abstraction will provide a more stable solution.

Colorblind Mode

If you remember, in part two we removed outlines from sprites because of their impracticality. At the time, we didn’t discuss the consequences of this choice but, if we think about it, not separating different color spots is potentially problematic for colorblind people.

Given the inherent visual nature of the concept, Syzygy is already hopelessly inaccessible for people who are blind, but we can still do something to ensure that everyone with a lesser visual impairment can still enjoy the experience.

Introducing a colorblind mode would have been a reasonable option but, instead, I decided to provide a one-size-fits-all color experience. To better understand the problem, we must first have a little bit of context.

In the human eye, color perception is carried out by a type of cell, called cone, which comes in three flavors; each one reacts differently to certain wavelengths and they are very broadly associated with primary additive colors: red, green or blue. The following picture shows cone sensibility for every type at varying wavelengths:

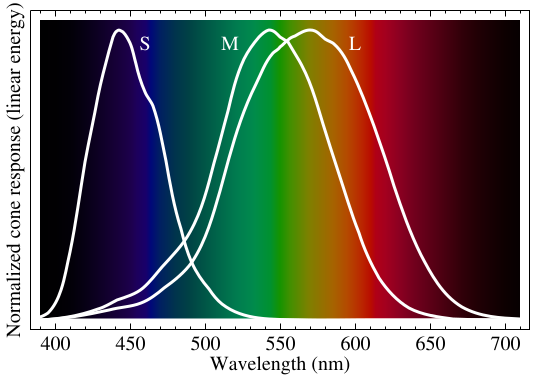
Partial or complete malfunctioning of one or more cone types is one of the causes for color blindness: depending on the damaged cells, different groups of colors tend to be confused. At the extreme, there is achromatopsia: none of the cones work properly and the person affected is sensible only to light intensity, which is perceived by different cells called rods.

From this last biological fact we can deduce that, on a logical level, the minimum subset for color perception is really light intensity. If we can make every color tone used in the game have a unique light intensity then it will be perfectly distinguishable by everyone with a color vision impairment.

This sounds easy when said, but it’s actually pretty hard to achieve. I basically spent a very long time tweaking colors to maximize their beauty for people with average color vision, while also turning them to grayscale once in a while to check if they were still distinguishable by someone who didn’t see color at all.

I also strove to never convey any information by color alone, adding other type of markers: one example is that floor tiles of different color have also different patterns on their surfaces.

In the following screenshots, I applied various filters to make the picture look as if seen through the eyes of people with different kind of color-blindness: as you can see, the level layout and the contained entities never get mixed up with one another.

Images produced by the useful Color Oracle.

In the end, the result was ok: I compromised a little on the color palette while gaining sprites that are almost always unique in terms of light intensity. There are little overlaps here and there, but nothing significant enough to impair the experience.

In retrospective, the activity was extremely time consuming and the outcome not outstanding enough to justify the effort: next time I will probably try to conjure a more automatic process to fix color palettes on the fly.

Resolution Independence

As we saw in part one, everything in Syzygy is a shape and is rendered as such. One nice consequence is freeing the game from the tie of fixed resolution that would trouble a normal pixel art game. Once the shapes are anti-aliased they look good at any resolution.

Add in the fact that the game levels are designed to fit in one screen and you can see why I couldn’t resist the temptation to make the whole game dynamically adapt to whatever resolution the user chooses.

Technically speaking, it is not hard to achieve: it is conceptually similar to a web page that has to be seen on a phone as well as on a desktop. Once you have checked the current level size against the screen dimension and resized the level accordingly, you just have to sensibly set the minimum and maximum proportions among elements: tiny text and UI shouldn’t be paired up with giant level tiles and sprites.

As web developers have probably known for a long time, it seems very hard to predetermine an algorithm that will resize everything sensibly all the times, so the best course of action is still to optimize the proportions for the most common screen ratios, leaving the really weird ones sub-optimal.

It is very funny and users may not even realize it, but it is possible to play the game in a very tall and thin window or in a very large one and everything in between. A cool side effect is that, with extreme screen ratios, it is possible to see a wider portion of the background, showing some real nice patterns.

We come to the end of our last article on the hardships met while working on the graphics of Syzygy. I thank you again for your time and I hope I have given you something to stir your mind.

I am also planning to write a companion piece on the sound programming of Syzygy so, if that might interest you, stay tuned and I’ll try to quench your curiosity.

body { text-align: justify; margin: 2em; } h1 { text-align: center; } h3 { text-align: center; font-style: italic; font-weight: normal; margin-top: 0.3em; margin-bottom: 1.5em; } em { font-weight: bold; font-style: italic; }

A few thoughts on the 0PLAYER game

You can trace the birth of puzzle video games as an extension of paper puzzle games and the line-tracing mechanic in The Witness (which is worth noting was not part of the original core idea of the game) was certainly taken from paper puzzle games.

With 0PLAYER, I feel that the whole process has come full circle and it also made clear in my mind why I have been feeling less and less compelled by puzzle games as time goes by. The thousands of PuzzleScript and non-PuzzleScript games that have sprung up in recent years can always be traced back to Stephen’s Sausage Roll (even games that predate its 2016 release).

Once you have played your Stephen’s Sausage Roll you have played them all: they don’t get better than that and they also don’t get far qualitatively. For PuzzleScript games in particular, this feels especially relevant in light of the fact that Increpare (Stephen Lavelle) is the creator of both Stephen’s Sausage Roll and PuzzleScript: wielders of his tools cannot escape the master’s gaze, so to speak.

They are all essentially games about puzzles and that’s why I have to leave out Braid and The Witness, which are not about puzzles but use the puzzle language to talk about something else completely. In the standard way of people doing their standard thing, only the superficial parts of Braid and The Witness were incorporated into public awareness. That’s why after so many years I am still fond of the flash game “One & One Story” by Mattia Traverso and I still think it’s the best italian video game to date (sadly): it captures more broadly the overall way of communicating through video games presented in Braid and it translates it into a slightly different domain, which is far beyond what most people did.

Stealing Braid’s own words, “when the cinema closes and most of the audience strolls down the plaza to the south, Tim goes north”: in the 17 years (yikes, what have I been doing all this time?) since its release, quite a few people have taken up the puzzle game language and developed it for puzzles’ sake; as if taking up the language of poetry everyone just worked on increasingly complex rhyming schemes while keeping the topic spasmodically fixated on what you ate for breakfast.

Don’t get me wrong, Stephen’s Sausage Roll is a pinnacle of technical game design and the world is a better place for it but, at the same time, it’s also a parlor trick that you can do only once: the second time it’s already stale.

That’s why everyone proceeded to make their own version a thousand times over.

Back to 0PLAYER, the reason why it stirs me so much even if I haven’t “played” it and I don’t intend to do so, is because it demonstrates that the process of video game puzzle making has rarefied itself to the point of disappearing.

A cardinal virtue of puzzle games is that of being legible in the sense that once you know the rules of the game you can play a level entirely in your head and only cursorily input the solution once you know it’s the right one. The other staple of puzzle video games is that of rule deduction, figuring out a mental model of the game world starting from the player’s interactions with the game. By magistrally ping-ponging back and forth between these two concepts Stephen’s Sausage Roll achieves peaks of design greatness where the player is constantly re-evaluating her actual capabilities inside the world while being presented with koan-like puzzles.

And I feel the tortuous difficulty, this sense of impossibility, is the third pole that keeps the whole structure afloat: that is why I was left with a bad taste in my mouth by games like Patrick’s Parabox, a feeling of disappointment and betrayal. What is the point of a cool and unexpected behaviour if when I see the puzzle that should trigger my understanding I can almost immediately say: Well, it’s probably that? If a puzzle does not feel impossible and I don’t have to progress via careful use of the scientific method, formulating hypothesis and testing them out, what is the actual reason for having a video game? If I can infer and run the whole machine inside my brain, what is the point of “playing”?

0PLAYER answers the question brilliantly by engraving a “none” onto the puzzle game tombstone.

Note that here Braid and The Witness actually do much more and keep the chain going: X is impossible because of Y, which implies Z, where Z is an actual useful consideration about the world we live in.

Since I still haven’t said it, it might be worth explaining that 0PLAYER is not a video game. It’s just a picture of the world map of a single-level imaginary puzzle game. Mechanics are simple and intuitive enough that you can pick them up by just looking at the puzzles and try to play the game in your head. The fact that you can jump from puzzle to puzzle by virtue of eye movement helps you form a complete understanding of the ruleset, which must satisfy all puzzles and contradict none. And there certainly are puzzles that look impossible, that force you to reconsider your working knowledge of the ruleset to add exceptions and loopholes.

So what does this all mean? What if at the pinnacle of puzzle video game design sophistication the final product is a paper puzzle? I don’t necessarily have a definitive answer to the questions I throw around (I would be an idiot otherwise), but I feel that the whole exercise has grown to become evidently masturbatory in nature.

Which sounds really stupid said by someone who essentially created two sokoban games, but in my defense I can say that my puzzle design skills are trash (which in the context of this argument seems like a virtue) and, even if it doesn’t look like it, I always worked with the ghost of Jonathan Blow in my mind, wanting to communicate more than just the bare video game world mechanics to the player. Fingers vaguely pointing toward the moon.

To summarize, both because I feel like I have been rambling and because my time is running out and I have to go do other stuff, while I don’t give even the slightest amount of fuck about playing 0PLAYER I am really fond of what it communicates by virtue of simply existing. A puzzle video game to end them all. We have developed a beautiful video game prose, maybe it’s time to start using it to actually say something of value, shall we?